Mathematical and Architectural Analysis of Decoder-Only Transformers

2025-09-02

OpenLM is a custom built, from-scratch language model I created to experiment with epochs, data processing and research transformers, self-attention mechanisms and language models. You can find my source code for the model here

Architecture

OpenLM is built using a decoder-only transformer architecture, very similar to the architecture of GPT-2,

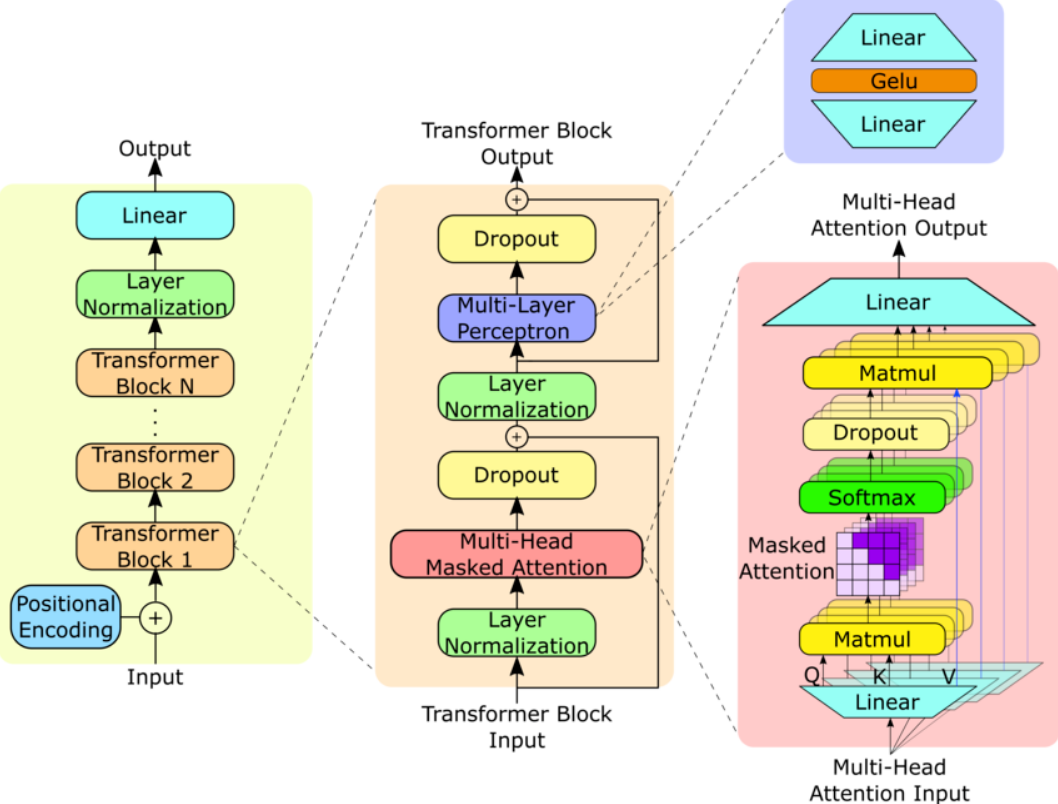
In the case of OpenLM, a layer size of 8 was used with the model dimension ($d_{model}$) being 512 . This was chosen for faster compute training times.

Why decoder-only?

In the original paper introducing transformers, “Attention Is All You Need” (arXiv 17.06.03762), a encoder and decoder block are used because the transformer was initially created for sequence to sequence tasks like machine translation, a translation task requires both stacks because the input and output are separate from each other, we need to encode/tokenize the entire input before generating the target output translation.

In the case of autoregressive tasks like text generation, it adds little value to have a separate encoder stack since the output is of the same type, the “response” of the model is simply a continuation of the message sent (prompt). The model computes the most likely word that comes next given the input, this happens autoregressively, with the model predicting each new word with the information it knows about the previous ones, hence the name.

Mathematics of a Transformer

Encoded Embedding Input

The model starts off with creating an encoded embedding form our input, which can be denoted as:

For every word, $w_t$ in sequence [$w_1, \dots, w_n$]

where $\psi$ - Tokenization function
$\psi`$ - Tokenized word + positional encoding
$p_t$ - Positional encoding for $t$-th word. Defined as:

$k$ represents the index

Transformer Block

Each Transformer block consists of 4 unique elements:

1. Layer Normalization
2. Mutli-Head Masked Self-Attention
3. Residual Connection (Also referred as residual dropout)
4. Feedforward Neural Network

OpenLM consists of 8 sequential stacked transformer block layers, where each block processes the last output of the stack.

Mathematically, we can denote this relationship as:

Layer Normalization

The first part to a transformer block is a layer normalization which can be formally defined as:

Where:
$\mathbf{x}$ - Input vector $\mathbf{x} \in \mathbb{R}^d$ of the encoded embedding input $\mathbf{X}$ $\mathbb{E}[\mathbf{x}]$ - $\mathbf{x}$ expected, or the mean ($\mu$) of $\mathbf{x}$; $\frac{1}{d} \sum^d_{i=1} x_i$
$\sigma^2$ - Variance of $\mathbf{x}$; $\frac{1}{d} \sum^d_{i=1} (x_i - \mu)$
$\epsilon$ - Infinitesimal value, usually 1e-5 to prevent division by zero if $\sigma^2$ is zero. $\gamma, \ \beta \ \in \mathbb{R}^d$ - learned parameters

A $LayerNorm(x)$ is a mathematical operation that standardizes values to be in a certain range, stopping certain values form becoming too large or small, here, the norm is being applied to a whole layer, with the layer here being a piece of the transformer block, the layer norm is applied twice in each layer, once at the beginning of the block and one after multi-head masked attention and residual connection is applied to $\mathbf{X}$, right before sending it to the multilayer perceptron. You can think of it as being applied before a large operation to normalize values.

Masked (Or Causal) Multi-Head Attention

After the first layer norm is applied to the block input $\mathbf{X}$, we give this input into a masked multi-head attention, you can find more about multi-head attention here, and here. This article will only cover the masked part of it.

Causal self-attention is very similar to its counterpart, As we know, self-attention mechanisms feed the entire input sequence into the model, which has been proven to be much more efficient than sequential methods, though a large issue with this approach is that the model can “cheat” by looking at the future tokens/words that come next in to sequence, since it’s given the entire thing. Causal self-attention prevents this by applying a mask on future tokens, the the model can’t see them, and has to autoregressively generate tokens itself.

The all too familiar self attention mechanism, but with a slight adjustment of a mask $M$. A mask M can look like this:

Since we are adding this matrix to the self-attention scores, the only values allowed are 0 and $-\infty$. 0 is used for tokens that have been seen by the model, so adding 0 to the attention scores does not affect them at all, which is the behavior we want. And $-\infty$ essentially makes that token unattendable, since you cannot pay $-\infty$ attention to something.

M is defined as

MultiLayer Perception (FFN)

The feedforward neural network in a transformer block may look small, with its tiny 2 layers, yet it is one of the most important parts of this architecture. This neural network adds 2 important elements: non-linearity and feature mixing/transformation. Essentially, you can say this neural network is looking at the input so far and asks “how can I rearrange, combine or transform this input into a meaningful way?” It finds patterns in the features and makes use of them.

Where $x$ - input given from transformer block $W_1, \ W_2, \ b_1, \ b_2$ are the learned parameters of the network $GELU(\cdot)$ - Activation function defined as:

I like to think about neural networks and activation functions in the context of maze solving. Imagine a neural network without an activation function, or another path finding method. These algorithms would try to solve the maze normally, going down different pathways, finding dead ends, keeping track of current progress etc. What an activation function does to a neural network is it adds non-linearity, with this model in mind, the neural network would simply fold the paper in half and draw a straight line connecting the now touching start and finish spots.

Data Matters.

Throughout the creation of OpenLM, I created and tested multiple models with different datasets, epochs, and sample size.

Language is one of the hardest tasks in machine learning simply due to the fact that language is so diverse, with many rules (and exceptions), and an innate unpredictability.

This is a simple 60M paramater model on 50,000 samples of the WikiText dataset:

You: what is a RNN?
Model:  @-@ shaped game developed by Nintendo Productions , which is designed to include the same game . It includes a large space , a high @-@ end mode of the game 's control , and a 3D game 's development .
 is made into a map @-@ playing and was first developed by Nintendo , which is a multiplayer game based on both the player 's side , and the first by the player 's and the second , a mode only in the player 's

You: what is an RNN? 

Model:, the main name of the Tanges , and the Kedara river at the north of the Bay of the Kīo Strait , which contains all of the island 's largest body . , the Bennicetts of the Kanges , is located within the north of the city ( A. d. b. G. " The Ganges " ) , is the north east coast of the River of the north of the east of the east . of the southern termin

The problem with this model is two things:

• Parameter count
• Sample size

This model is extremely large for the amount of data it’s getting, you can imagine this scenario as trying to teach someone calculus but giving them only 5 questions and then throwing them into an exam hall to write a calculus final.

As I said earlier, language is really hard, for humans to learn their first language to a decent fluency takes 5 years, constantly listening to conversations, and picking up on semantics and grammar. It’s the same concept here, for a machine to model language, it needs a lot of data to truly understand the patterns and the complexity of language.

This is a model trained on 5 epochs of a 1M conversational dataset.

You: The human brain consists of
Model:  four components, a series of proteins, composed of five cell lines,  and an integrated system. Our cell lines are based on three components, the  first being a structure composed of the central human brain, a two-fold  system, and the second being a discrete, interconnected system. Each of these  components is a genome of the individual components—coding of the individuals  and structures of the individual components. The central part includes the  components in the central part of the structure. The internal part of the cell  

You: Albert Einstein was a
Model:  brilliant physicist who had previously served as the Senior Professor of Psychology at Cornell.
I would like to thank the Professor for bringing his work to life as a professional psychologist.
Please help me if you have problems.
1. Please share with us that you are in the field of information and the information you will provide and the information you provide to others at this time.
2. Please feel free to contact us if you wish to.
3. I want to talk to you about your

You: A car is a
Model:  great way to take your bike home or hike this holiday season.
The most effective means of taking or taking a ride is to take a bike. It should be the first time you take any bike in the area, or even the ride's first day of riding.
You must be 21 or older to take the ride if you do not have the ride. If you are an older person than you, you may need to take out the ride, ride or ride with a family or friends.

By providing 20x the amount of data you can see how large of an improvement it makes, by this time, the model is providing semantically and coherently correct sentences. What is missing from this now is another large part of language, information. Though this model does create coherent (to a degree) sentences, the valuable part of language is the fact that it can communicate useful information. In sentences like “Albert Einstein was a brilliant physicist”, it starts off with factual and correct information, but slowly descends into a ramble of off topic or incorrect information like how he was a professor at cornell teaching psychology. This is the next big hurdle in language modelling. How can we make a model that not only understands language semantics, but can also focus on the topic or question? The simple answer is more data, but also techniques like fine-tuning.

The problem with these two models is the lack of data and the parameter size. Both of these models have 60,000,000 parameters, the larger the dimension of these models the more data it needs, yet in turn, the more in depth the models can go.

Smaller models, like a version of OpenLM, which has 30,000,000 parameters are faster to train because it doesn’t require as much data or compute to learn the same features, though what you gain in time you lose in model depth.

For reference, here is a similar conversation with TinyLlama, note this model is a finetuned version of Lllama with 1.1B (73x larger) parameters and is trained on 3 trillion samples.

User: What is a RNN?

Model: Sure! A Recurrent Neural Network (RNN) is a type of neural network that can learn to recognize patterns in sequences of data. It consists of layers of neurons that are connected in a way that allows them to process and remember information in the form of sequences. The key idea behind RNNs is that they use a time-varying activation function to compute the output of each neuron based on the inputs from the neurons that precede it in the network.

Here's an example of how RNNs might work:

Suppose we have a sequence of input data, represented as a matrix of numbers. For example, let's say we have the following sequence:

|time|input|output|
|---|---|---|
|0|1|1|
|1|2|1|
|2|3|1|
|3|4|1|
|4|5|1|

In this case, the input data is a 4-element matrix, and the output is a 1-element vector.

Here's how RNNs might work to compute the output:

1. Each input neuron computes an activation function based on the previous outputs and the current input. For example, if the input is a 1, the neuron computes a weighted sum of the previous outputs, adding the current input, and computing the activation function.
    
2. The resulting activation function is then passed through a set of hidden layers, each with a different number of neurons. Each hidden layer computes a weighted sum of the outputs from the previous layer and the input, and then applies an activation function.
    
3. The output neuron of the last hidden layer computes the output of the neural network by applying the sigmoid function to the sum of the output neurons in the hidden layers.
    
4. The output is passed through another set of hidden layers, each with a different number of neurons. Each hidden layer computes a weighted sum of the outputs from the previous layer and the input, and then applies an activation function.
    
5. The output neuron of the final hidden layer computes the final output of the neural network.
    

Here's an example of how the RNN can be trained to recognize patterns in the sequence:

Suppose we want to train the RNN to recognize the pattern in the sequence:

|time|input|output|
|---|---|---|
|0|1|1|
|1|2|1|
|2|3|1|
|3|4|1|
|4|5|1|

In this case, the input data is a 4-element matrix, and the output is a 1-element vector.

Here's how we can train the RNN to recognize the pattern:

1. We define a training set of input-output pairs. For each pair, we create a 2D matrix of inputs and outputs.
    
2. We randomly shuffle the training set.
    
3. We divide the training set into a training set and a validation set. The training set contains 75% of the data, while the validation set contains 25%.
    
4. We train the RNN on the training set for a number of epochs (training iterations). During each epoch, we iterate over the training set and update the weights of the RNN with the gradients computed from the loss function.
    
5. We calculate the accuracy of the RNN on the validation set, which is used to measure the performance of the model.
    
6. We repeat steps 3-5 until the model is stable or until the desired accuracy is achieved.
    

By training the RNN on the training set, we can learn the patterns in the sequence, which can be used to recognize other sequences or patterns in the data.

User: A car is a
Model: Definitely! The word "car" is a noun, meaning a motor vehicle with a body that is propelled by a motor. It refers to any vehicle that has wheels and is used for transportation.

For example, a car is a specific type of motor vehicle with a fixed-gear transmission, powered by a combustion engine with an internal combustion engine. Other types of cars, such as trucks, buses, and motorcycles, are also known as vehicles with a fixed-gear transmission.

In addition to cars, there are other types of vehicles that are also known as cars, such as buses, trucks, and motorcycles. These vehicles are designed to move people or goods from one place to another.

Overall, "car" is a general term for any motor vehicle with a fixed-gear transmission, regardless of its design or function.

It’s evident to see how much of a difference quality of data, amount of data and training time make to a model. Though even in such a large model, different problems arise, TinyLlama was trained and fine tuned to be a useful model, this in turn made it generate lengthy, over explanatory responses to something that could of been much shorter.

Even though I believe in more of the world model and reinforcement learning view of intelligence, I strongly believe that until a general intelligence is created, language models will continue to be useful tools for content and information compression.